Multi-Res Modeling Group People Research


Teaching		 Publications Software
Multi-Res Modeling Group Multi-Res Modeling Group

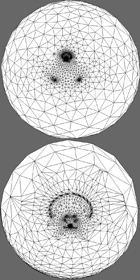
Gallery of globally optimal direction fields with or without guidance field. Globally Optimal Direction Fields (Felix Knöppel, Keenan Crane, Ulrich Pinkall, Peter Schröder), ACM Transcations on Graphics, 32(4), 2013. Abstract: We present a method for constructing smooth n-direction fields (line fields, cross fields, etc.) on surfaces that is an order of magnitude faster than state-of-the-art methods, while still producing fields of equal or better quality. Fields produced by the method are globally optimal in the sense that they minimize a simple, well-defined quadratic smoothness energy over all possible configurations of singularities (number, location, and index). The method is fully automatic and can optionally produce fields aligned with a given guidance field such as principal curvature directions. Computationally the smoothest field is found via a sparse eigenvalue problem involving a matrix similar to the cotan-Laplacian. When a guidance field is present, finding the optimal field amounts to solving a single linear system.

Smoothing flows can be filtered in the frequency domain to achieve a variety of effects. Robust Fairing via Conformal Curvature Flow (Keenan Crane, Ulrich Pinkall, Peter Schröder), ACM Transcations on Graphics, 32(4), 2013. Abstract: We present a formulation of Willmore flow for triangulated surfaces that permits extraordinarily large time steps and naturally preserves the quality of the input mesh. The main insight is that Willmore flow becomes remarkably stable when expressed in curvature space -- we develop the precise conditions under which curvature is allowed to evolve. The practical outcome is a highly efficient algorithm that naturally preserves texture and does not require remeshing during the flow. We apply this algorithm to surface fairing, geometric modeling, and construction of constant mean curvature (CMC) surfaces. We also present a new algorithm for length-preserving flow on planar curves, which provides a valuable analogy for the surface case.

image Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow (Keenan Crane, Clarisse Weischedel, Max Wardetzky), ACM Transcations on Graphics, 2013. Abstract: We introduce the heat method for computing the geodesic distance to a specified subset (e.g., point or curve) of a given domain. The heat method is robust, efficient, and simple to implement since it is based on solving a pair of standard linear elliptic problems. The resulting systems can be prefactored once and subsequently solved in near-linear time. In practice, distance is updated an order of magnitude faster than with state-of-the-art methods, while maintaining a comparable level of accuracy. The method requires only standard differential operators and can hence be applied on a wide variety of domains (grids, triangle meshes, point clouds, etc.). We provide numerical evidence that the method converges to the exact distance in the limit of refinement; we also explore smoothed approximations of distance suitable for applications where greater regularity is required.

On top a standard normal displacement which suffers from typical distortion artifacts. Below a conformal displacement which does not exhibit shearing in the texture. Spin Transformations of Discrete Surfaces (Keenan Crane, Ulrich Pinkall, Peter Schröder), ACM Transcations on Graphics, 30(4), 2011. Abstract: We introduce a new method for computing conformal transformations of triangle meshes in R3. Conformal maps are desirable in digital geometry processing because they do not exhibit shear, and therefore preserve texture fidelity as well as the quality of the mesh itself. Traditional discretizations consider maps into the complex plane, which are useful only for problems such as surface parameterization and planar shape deformation where the target surface is flat. We instead consider maps into the quaternions H, which allows us to work directly with surfaces sitting in R3. In particular, we introduce a quaternionic Dirac operator and use it to develop a novel integrability condition on conformal deformations. Our discretization of this condition results in a sparse linear system that is simple to build and can be used to efficiently edit surfaces by manipulating curvature and boundary data, as demonstrated via several mesh processing applications.

Artistic renditions of some direction fields designed with our algorithm. Trivial Connections on Discrete Surfaces (Keenan Crane, Mathieu Desbrun, Peter Schröder), Computer Graphics Forum, 29(5), 2010, pp 1525-1533. Abstract: This paper presents a straightforward algorithm for constructing connections on discrete surfaces that are as smooth as possible everywhere but on a set of isolated singularities with given index. We compute these connections by solving a single linear system built from standard operators. The solution can be used to design rotationally symmetric direction fields with user-specified singularities and directional constraints.

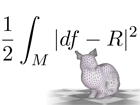The core theme of the paper is the distance of a deformation from the rotation group as an energy. All else follows (including the bunny). A Simple Geometric Model for Elastic Deformations (Isaac Chao, Ulrich Pinkall, Patrick Sanan, Peter Schröder), ACM Transactions on Graphics, 29(4), 2010, 38:1-38:6. Abstract: We advocate a simple geometric model for elasticity: distance between the differential of a deformation and the rotation group. It comes with rigorous differential geometric underpinnings, both smooth and discrete, and is computationally almost as simple and efficient as linear elasticity. Owing to its geometric non-linearity, though, it does not suffer from the usual linearization artifacts. A material model with standard elastic moduli (Lame parameters) falls out naturally, and a minimizer for static problems is easily augmented to construct a fully variational 2nd order time integrator. It has excellent conservation properties even for very coarse simulations, making it very robust. Our analysis was motivated by a number of heuristic, physics-like algorithms from geometry processing (editing, morphing, parameterization, and simulation). Starting with a continuous energy formulation and taking the underlying geometry into account, we simplify and accelerate these algorithms while avoiding common pitfalls. Through the connection with the Biot strain of mechanics, the intuition of previous work that these ideas are "like" elasticity is shown to be spot on.

Topological sphere with 14 automatically placed and optimized cone singularities Conformal Equivalence of Triangle Meshes (Boris Sprinborn, Peter Schröder, Ulrich Pinkall), ACM Transactions on Graphics, 27(3), 2008, 77:1-77:11. Abstract: We present a new algorithm for conformal mesh parameterization. It is based on a precise notion of discrete conformal equivalence for triangle meshes which mimics the notion of conformal equivalence for smooth surfaces. The problem of finding a flat mesh that is discretely conformally equivalent to a given mesh can be solved efficiently by minimizing a convex energy function, whose Hessian turns out to be the well known cot-Laplace operator. This method can also be used to map a surface mesh to a parameter domain which is flat except for isolated cone singularities, and we show how these can be placed automatically in order to reduce the distortion of the parameterization. We present the salient features of the theory and elaborate the algorithms with a number of examples.

Vector fields designed for the VW and horse were used in anisotropic texture synthesis. Design of Tangent Vector Fields (Matthew Fisher, Peter Schröder, Mathieu Desbrun, Hugues Hoppe), ACM Transactions on Graphics, 27(3), 2007. Abstract: Tangent vector fields are an essential ingredient in controlling surface appearance for applications ranging from anisotropic shading to texture synthesis and non-photorealistic rendering. To achieve a desired effect one is typically interested in smoothly varying fields that satisfy a sparse set of user-provided constraints. Using tools from Discrete Exterior Calculus, we present a simple and efficient algorithm for designing such fields over arbitrary triangle meshes. By representing the field as scalars over mesh edges (i.e., discrete 1-forms), we obtain an intrinsic, coordinate-free formulation in which field smoothness is enforced through discrete Laplace operators. Unlike previous methods, such a formulation leads to a linear system whose sparsity permits efficient pre-factorization. Constraints are incorporated through weighted least squares and can be updated rapidly enough to enable interactive design, as we demonstrate in the context of anisotropic texture synthesis.

Running Quantum Monte Carlo chemistry simulations on a GPU can lead to significant performance gains and far better performance/cost compared to a CPU implementation. Quantum Monte Carlo on Graphical Processing Units (Amos Anderson, William A. Goddard III, Peter Schröder), Computer Physics Communications, 177(3), pp 298-306. Abstract: Quantum Monte Carlo (QMC) is among the most accurate methods for solving the time independent Schrödinger equation. Unfortunately, the method is very expensive and requires a vast array of computing resources in order to obtain results of a reasonable convergence level. On the other hand, the method is not only easily parallelizable across CPU clusters, but as we report here, it also has a high degree of data parallelism. This facilitates the use of recent technological advances in Graphical Processing Units (GPUs), a powerful type of processor well known to computer gamers. In this paper we report on an end-to-end QMC application with core elements of the algorithm running on a GPU. With individual kernels achieving as much as 30x speed up, the overall application performs at up to 6x relative to an optimized CPU implementation, yet requires only a modest increase in hardware cost. This demonstrates the speedup improvements possible for QMC in running on advanced hardware, thus exploring a path toward providing QMC level accuracy as a more standard tool. The major current challenge in running codes of this type on the GPU arises from the lack of fully compliant IEEE floating point implementations. To achieve better accuracy we propose the use of the Kahan summation formula in matrix multiplications. While this drops overall performance, we demonstrate that the proposed new algorithm can match CPU single precision.

Spherical parameterization of the Triceratops model; top: Tutte weights; bottom: discrete harmonic. Unconstrained Spherical Parameterization (Ilja Friedel, Peter Schröder, Mathieu Desbrun), Journal of Graphics Tools, 12(1), 2006, pp. 17-26. Abstract: We introduce a novel approach for the construction of spherical parameterizations based on energy minimization. The energies are derived in a general manner from classic formulations well known in the planar parameterization setting (e.g., conformal, Tutte, area, stretch energies, etc.), based on the following principles: the energy should (1) be a measure of spherical triangles; (2) treat energies independently of the triangle location on the sphere; and (3) converge to the continuous energy from above under refinement. Based on these considerations we give a very simple non-linear modification of standard formulas that fulfills all these requirements. The method avoids the usual collapse of flat energies when they are transferred to the spherical setting without additional constraints (e.g., fixing three or more vertices). Our unconstrained energy minimization problem is amenable to the use of standard solvers. Consequently the implementation effort is minimal while still achieving excellent robustness and performance through the use of widely available numerical minimization software.

Frames from a simulation of fluid within a snow globe. State, Circulation-Preserving, Simplicial Fluids (Sharif Elcott, Yiying Tong, Eva Kanso, Peter Schröder, and Mathieu Desbrun), ACM Transactions on Graphics, 26(1). Abstract: Visual quality, low computational cost, and numerical stability are foremost goals in computer animation. An important ingredient in achieving these goals is the conservation of fundamental motion invariants. For example, rigid and deformable body simulation benefits greatly from conservation of linear and angular momenta. In the case of fluids, however, none of the current techniques focuses on conserving invariants, and consequently, they often introduce a visually disturbing numerical diffusion of vorticity. Visually just as important is the resolution of complex simulation domains. Doing so with regular (even if adaptive) grid techniques can be computationally delicate. In this paper, we propose a novel technique for the simulation of fluid flows. It is designed to respect the defining differential properties, i.e., the conservation of circulation along arbitrary loops as they are transported by the flow. Consequently, our method offers several new and desirable properties: arbitrary simplicial meshes (triangles in 2D, tetrahedra in 3D) can be used to define the fluid domain; the computations involved in the update procedure are efficient due to discrete operators with small support; and it preserves discrete circulation avoiding numerical diffusion of vorticity.

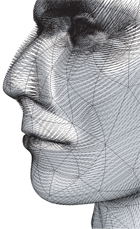
Frame from a simulation of elastic material. Geometric, Variational Integrators for Computer Animation (Liliya Kharevych, Weiwei, Yiying Tong, Eva Kanso, Jerrold E. Marsden, Peter Schröder, Mathieu Desbrun), SCA 2006. Abstract: We present a general-purpose numerical scheme for time integration of Lagrangian dynamical systems - an important computational tool at the core of most physics-based animation techniques. Several features make this particular time integrator highly desirable for computer animation: it numerically preserves important invariants, such as linear and angular momenta; the symplectic nature of the integrator also guarantees a correct energy behavior, even when dissipation and external forces are added; holonomic constraints can also be enforced quite simply; finally, our simple methodology allows for the design of high-order accurate schemes if needed. Two key properties set the method apart from earlier approaches. First, the nonlinear equations that must be solved during an update step are replaced by a minimization of a novel functional, speeding up time stepping by more than a factor of two in practice. Second, the formulation introduces additional variables that provide key flexibility in the implementation of the method. These properties are achieved using a discrete form of a general variational principle called the Pontryagin-Hamilton principle, expressing time integration in a geometric manner. We demonstrate the applicability of our integrators to the simulation of non-linear elasticity with implementation details.

Designing smoothly varying tangent vector fields over subdivision surfaces becomes easy with our novel discrete differential 1-form subdivision scheme. Edge Subdivision Schemes and the Construction of Smooth Vector Fields (Ke Wang, Weiwei, Yiying Tong, Mathieu Desbrun, Peter Schröder), ACM Transactions on Graphics, 25(3). Abstract: Vertex- and face-based subdivision schemes are now routinely used in geometric modeling and computational science, and their primal/dual relationships are well studied. In this paper, we interpret these schemes as defining bases for discrete differential 0- resp. 2-forms, and complete the picture by introducing edge-based subdivision schemes to construct the missing bases for discrete differential 1-forms. Such subdivision schemes map scalar coefficients on edges from the coarse to the refined mesh and are intrinsic to the surface. Our construction is based on treating vertex-, edge-, and face-based subdivision schemes as a joint triple and enforcing that subdivision commutes with thetopological exterior derivative. We demonstrate our construction for the case of arbitrary topology triangle meshes. Using Loop's scheme for 0-forms and generalized half-box splines for 2-forms results in a unique generalized spline scheme for 1-forms, easily incorporated into standard subdivision surface codes. We also provide corresponding boundary stencils. Once a metric is supplied, the scalar 1-form coefficients define a smooth tangent vector field onthe underlying subdivision surface. Design of tangent vector fields is made particularly easy with this machinery as we demonstrate.

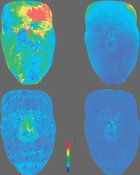
Error comparison of parameterization results with extrinsic (left column) versus intrinsic (right column) Laplace-Beltrami operator for Dirichlet (top row) and Neumann (bottom row) boundary conditions. An Algorithm for the Construction of Intrinsic Delaunay Triangulations with Applications to Digital Geometry Processing (Matthew Fisher, Boris Springborn, Alexander I. Bobenko, Peter Schröder), Computing, 82(2-3), 2007, pp 199-213. Abstract: The discrete Laplace-Beltrami operator plays a prominent role in many Digital Geometry Processing applications ranging fromdenoising to parameterization, editing, and physical simulation. The standard discretization uses the cotangents of the angles in the immersed mesh which leads to a variety of numerical problems. We advocate use of the intrinsic Laplace-Beltrami operator. It satisfies a local maximum principle, guaranteeing, e.g., that no flipped triangles can occur in parameterizations. It also leads to better conditioned linear systems. The intrinsic Laplace-Beltrami operator is based on an intrinsic Delaunay triangulation of the surface. We give an incremental algorithm to construct such triangulations together with an overlay structure which captures the relationship between the extrinsic and intrinsic triangulations. Using a variety of example meshes we demonstrate the numerical benefits of the intrinsic Laplace-Beltrami operator.

Higher dimensional intrinsic volumes can all be reduced to the most fundamental measure: the Euler charasteristic. What Can We Measure? (Peter Schröder), in Course Notes on Discrete Differential Geometry. Abstract: Geometric integration provides the right tools to discuss generalizations of curvature integrals over surfaces and volumes independent of smoothness questions. A central role in this development is played by the intrinsic volumes giving rise to Hadwiger's theorem that all rigid motion invariant measures which are additive and continuous in the limit must be a formed by a linear combination of the intrinsic volumes. This machinery is directly useful for computations and corresponds closely to the kinds of measurements which serve as the basis for physical theories of the behavior of shapes.

With high level data structures it becomes easy to manage all the incidence relations in a simplicial complex. Building Your Own DEC at Home (Sharif Elcott and Peter Schröder), in Course Notes on Discrete Differential Geometry. Abstract: Using high level data structures it becomes easy to implement all the necessary machinery for performing computations over simplicial complexes using ideas from DEC. This tutorial provides a guide for the ideas behind such an implementation. (The code is available.)

Using the exp and log maps we construct manifold valued wavelets in the tangent space. Multiscale Representations for Manifold-Valued Data (Inam Ur Rahman, Iddo Drori, Victoria C. Stodden, David L. Donoho, Peter Schröder), appeared in SIAM Multiscale Modeling and Simulation. Abstract: We describe multiscale representations for data observed on equispaced grids and taking values in manifolds such as: the sphere S2, the special orthogonal group SO(3), the positive definite matrices SPD(n), and the Grassmann manifolds G(n, k). The representations are based on the deployment of Deslauriers-Dubuc and Average-Interpolating pyramids in the tangent plane of such manifolds, using the Exp and Log maps of those manifolds. The representations provide wavelet coefficients which can be thresholded, quantized, and scaled much as traditional wavelet coefficients. Tasks such as compression, noise removal, contrast enhancement, and stochastic simulation are facilitated by this representation. The approach applies to general manifolds, but is particularly suited to the manifolds we consider, i.e., Riemannian symmetric spaces, such as Sn-1, SO(n), G(n, k), where the Exp and Log maps are effectively computable. Applications to manifold-valued data sources of a geometric nature (motion, orientation, diffusion) seem particularly immediate. A software toolbox, SymmLab, can reproduce the results discussed in this paper.

The discrete Willmore energy is a function of the angles triangle circumcircles make with one another. Discrete Willmore Flow (Alexander Bobenko & Peter Schröder), Symposium on Geometry Processing, 2005, pp 101-110. Abstract: The Willmore energy of a surface, i.e., the integral of H2-K over the surface, being a function of mean and Gaussian curvature, captures the deviation of a surface from (local) sphericity. As such this energy and its associated gradient flow play an important role in digital geometry processing, geometric modeling, and physical simulation. In this paper we consider a discrete Willmore energy and its flow. In contrast to traditional approaches it is not based on a finite element discretization, but rather on an ab initio discrete formulation which preserves the Möbius symmetries of the underlying continuous theory in the discrete setting. We derive the relevant gradient expressions including a linearization (approximation of the Hessian), which are required for non-linear numerical solvers. As examples we demonstrate the utility of our approach for surface restoration, n-sided hole filling, and non-shrinking surface smoothing.

DNA design if facilitated through the use of tangible tools. Immersive Design of DNA Molecules with a Tangible Interface (Steven Schkolne, Hiroshi Ishii, and Peter Schröder), appeared in Proceedings of Visualization 2004. Abstract: This paper presents an experimental immersive interface for designing DNA components for application in nanotechnology. While much research has been done on immersive visualization, this is one of the first systems to apply advanced interface techniques to a scientific design problem. This system uses tangible 3D input devices (tongs, a raygun, and a multipurpose handle tool) to create and edit a purely digital representation of DNA. The tangible controllers are associated with functions (not data) while a virtual display is used to render the model. This interface was built in collaboration with a research group investigating the design of DNA tiles. A user study shows that scientists find the immersive interface more satisfying than a 2D interface due to the enhanced understanding gained by directly interacting with molecules in 3D space.

The correspondence generated between two surfaces by our algorithmn is used to transfer a texture and create a blend. An Image Processing Approach to Surface Matching (Nathan Litke, Marc Droske, Martin Rumpf and Peter Schröder), Proceedings of the Symposium on Geometry Processing 2005. Abstract: Establishing a correspondence between two surfaces is a basic ingredient in many geometry processing applications. Existing approaches, which attempt to match two meshes directly in 3D, can be cumbersome to implement and it is often hard to produce accurate results in a reasonable amount of time. In this paper, we present a new variational method for matching surfaces that addresses these issues. Instead of matching two surfaces directly in 3D, we apply well-established matching methods from image processing in the parameter domains of the surfaces. A matching energy is introduced that can depend on curvature, feature demarcations or surface textures, and a regularization energy controls length and area changes in the induced non-rigid deformation between the two surfaces. The metric on both surfaces is properly incorporated into the formulation of the energy. This approach reduces all computations to the 2D setting while accounting for the original geometries. Consequently a fast multiresolution numerical algorithm for regular image grids can be used to solve the global optimization problem. The final algorithm is robust, generically much simpler than direct matching methods, and very fast for highly resolved triangle meshes.

A surface parameterization is a map between two surfaces. Efficient variational methods are used to generate these maps by performing the computations in 2D. Variational Methods in Surface Parameterization (Nathan Litke), Ph.D. thesis, Caltech June 2005. Abstract: A surface parameterization is a function that maps coordinates in a 2-dimensional parameter space to points on a surface. This thesis investigates two kinds of parameterizations for surfaces that are disc-like in shape. The first is a map from a region of the plane to the surface. The second is a mapping from one surface to another, which defines a correspondence between them. The main challenge in both cases is the construction of a smooth map with low distortion. This thesis presents a variational approach to surface parameterization that addresses these challenges.

Discrete, Circulation-preserving, and Stable Simplicial Fluids (Sharif Elcott), MS thesis, Caltech May 2005. Abstract: Visual quality, low computational cost, and numerical stability are foremost goals in computer animation. An important ingredient in achieving these goals is the conservation of fundamental motion invariants. For example, rigid and deformable body simulation has benefited greatly from conservation of linear and angular momenta. In the case of fluids, however, none of the current techniques focuses on conserving invariants, and consequently they often introduce a visually disturbing numerical diffusion of vorticity. Visually just as important is the resolution of complex simulation domains. Doing so with regular (even if adaptive) grid techniques can be computationally delicate. In this thesis we describe a novel technique for the simulation of fluid flows. It is designed to respect the defining differential properties, i.e., the conservation of circulation along arbitrary loops as they are transported by the flow. Consequently, our method offers several new and desirable properties: (1) arbitrary simplicial meshes (triangles in 2D, tetrahedra in 3D) can be used to define the fluid domain; (2) the computations are efficient due to discrete operators with small support; (3) the method is stable for arbitrarily large time steps; (4) it preserves discrete circulation avoiding numerical diffusion of vorticity; and (5) its implementation is straightforward.

Max Planck head model and genus one letter A model are textured using conformal parameterizations with cone singularities. Discrete Conformal Mappings via Circle Patterns (Liliya Kharevych, Boris Springborn, and Peter Schröder), ACM TOG 25(2). Abstract: We introduce a novel method for the construction of discrete conformal mappings from surface meshes of arbitrary topology to the plane. Our approach is based on circle patterns, i.e., arrangements of circles - one for each face - with prescribed intersection angles. Given these angles the circle radii follow as the unique minimizer of a convex energy. The method supports very flexible boundary conditions ranging from free boundaries to control of the boundary shape via prescribed curvatures. Closed meshes of genus zero can be parameterized over the sphere. To parameterize higher genus meshes we introduce cone singularities at designated vertices. The parameter domain is then a piecewise Euclidean surface. Cone singularities can also help to reduce the often very large area distortion of global conformal maps to moderate levels. Our method involves two optimization problems: a quadratic program and the unconstrained minimization of the circle pattern energy. The latter is a convex function of logarithmic radius variables with simple explicit expressions for gradient and Hessian.

Variational Normal Meshes

Variational Normal Meshes (Ilja Friedel, Andrei Khodakovsky and Peter Schröder), ACM Transactions on Graphics, October 2004. Abstract: Hierarchical representations of surfaces have many advantages for digital geometry processing applications. Normal meshes are particularly attractive since their level to level displacements are in the local normal direction only. Consequently they only require scalar coefficients to specify. In this paper we propose a novel method to approximate a given mesh with a normal mesh. Instead of building an associated parameterization on the fly we assume a globally smooth parameterization at the beginning and cast the problem as one of perturbing this parameterization. Controlling the magnitude of this perturbation gives us explicit control over the range between fully constrained (only scalar coefficients) and unconstrained (3-vector coefficients) approximations. With the unconstrained problem giving the lowest approximation error we can thus characterize the error cost of normal meshes as a function of the number of non-normal offsets—we find a significant gain for little (error) cost. Because the normal mesh construction creates a geometry driven approximation we can replace the difficult geometric distance minimization problem with a much simpler least squares problem. This variational approach reduces magnitude and structure (aliasing) of the error further. Our method separates the parameterization construction into an initial setup followed only by subsequent perturbations, giving us an algorithm which is far simpler to implement, more robust, and significantly faster.


The parameter domain and a texture map of a variationally-optimal parameterization, which balances length, area and angle distortion Axioms and Variational Problems in Surface Parameterization (Ulrich Clarenz, Nathan Litke and Martin Rumpf), Computer Aided Geometric Design. Abstract: For a surface patch on a smooth, two-dimensional surface in R3, low-distortion parameterizations are described in terms of minimizers of suitable energy functionals. Appropriate distortion measures are derived from principles of rational mechanics, closely related to the theory of non-linear elasticity. The parameterization can be optimized with respect to the varying importance of conformality, length preservation and area preservation. A finite element discretization is introduced and a constrained Newton method is used to minimize a corresponding discrete energy. Results of the new approach are compared with other recent parameterization methods.

SURF 2003 In 2003 we had four students take part in Caltech's Summer Undergraduate Research Fellowships (SURF) program each of whom collaborated with Peter to define and develop a project. Jessica Gray chose to cover Time Lapse of Frog Embryo Development from MRI Data, Xie Yuan focused on 3D Bridge Construction, Pankhudi on Construction and Manipulation of DNA tiles in free space and Julia Ma explored different subdivision methods for free-form surface design. Each of these students gave an excellent oral presentation of their research at the SURF Seminar Day October 18th, 2003.

Reconstruction of Mt. St. Helens from contour lines C1-continuous Terrain Reconstruction from Sparse Contours (Kai Hormann, Salvatore Spinello, and Peter Schröder), Proceedings of Vision, Modeling, and Visualization 2003. Abstract: Contour lines from topographic maps are still the most common form of elevation data for the Earth's surface and in the case of historical landscapes, they often are the only available source of information. In this paper we present a new contour interpolation method that solves this bivariate problem by considering univariate curve interpolation along the approximate gradient directions of the unknown surface. For a point between two contours the height value is computed with Hermite interpolation based on the shortest distances to the contours and height and derivative information at the contours. The surfaces generated are C1 except at terrain characteristics such as ridges and valleys which are reconstructed as sharp features. The method also faithfully reconstructs summits, pits, and saddles and is especially well-suited for sparse sets of contours. The approach allows for an efficient numerical implementation as we demonstrate with a number of examples.

Models for parameterization Multilevel Solvers for Unstructured Surface Meshes (Burak Aksoylu, Andrei Khodakovsky and Peter Schröder), SIAM J. Sci. Comput., pp 1146-1165, 26(4), 2005. Abstract: Parameterization of unstructured surface meshes is of fundamental importance in many applications of Digital Geometry Processing. Such parameterization approaches give rise to large and exceedingly ill-conditioned systems which are difficult or impossible to solve without the use of sophisticated multilevel preconditioning strategies. Since the underlying meshes are very fine to begin with, such multilevel preconditioners require mesh coarsening to build an appropriate hierarchy. In this paper we consider several strategies for the construction of hierarchies using ideas from mesh simplification algorithms used in the computer graphics literature. We introduce two novel hierarchy construction schemes and demonstrate their superior performance when used in conjunction with a multigrid preconditioner. A comprehensive performance analysis of multigrid, hierarchical basis multigrid, and BPX-like preconditioners coupled with such hierarchy is also presented.

Globally smooth parameterization of a genus-2 surface Globally Smooth Parameterizations with Low Distortion (Andrei Khodakovsky, Nathan Litke and Peter Schröder), SIGGRAPH 2003. Abstract: Good parameterizations are of central importance in many digital geometry processing tasks. Typically the behavior of such processing algorithms is related to the smoothness of the parameterization and how much distortion it contains. Since a parameterization maps a bounded region of the plane to the surface, a parameterization for a surface which is not homeomorphic to a disc must be made up of multiple pieces. We present a novel parameterization algorithm for arbitrary topology surface meshes which computes a globally smooth parameterization with low distortion. We optimize the patch layout subject to criteria such as shape quality and metric distortion, which are used to steer a mesh simplification approach for base complex construction. Global smoothness is achieved through simultaneous relaxation over all patches, with suitable transition functions between patches incorporated into the relaxation procedure. We demonstrate the quality of our parameterizations through numerical evaluation of distortion measures and the excellent rate distortion performance of semi-regular remeshes produced with these parameterizations. The numerical algorithms required to compute the parameterizations are robust and run on the order of minutes even for large meshes.

Frames from a Navier-Stokes solver running in real time on the GeForce FX Sparse Matrix Solvers on the GPU: Conjugate Gradients and Multigrid (Jeff Bolz, Ian Farmer, Eitan Grinspun and Peter Schröder),SIGGRAPH 2003. Abstract: Many computer graphics applications require high-intensity numerical simulation. We show that such computations can be performed efficiently on the GPU, which we regard as a full function streaming processor with high floating-point performance. We implemented two basic, broadly useful, computational kernels: a sparse matrix conjugate gradient solver and a regular-grid multigrid solver. Realtime applications ranging from mesh smoothing and parameterization to fluid solvers and solid mechanics can greatly benefit from these, evidence our example applications of geometric flow and fluid simulation running on NVIDIA's GeForce FX using geometric flow (cube smoothing movie, 3D photography scan denoising movie) and fluid simulation (particle advection movie) as application examples.

Adaptive octree approximation of the horse model to level 3 Progressive Encoding of Complex Isosurfaces (Haeyoung Lee, Mathieu Desbrun, Peter Schröder),SIGGRAPH 2003. Abstract: Some of the largest and most intricate surfaces result from isosurface extraction of volume data produced by 3D imaging modalities and scientific simulations. Such surfaces often possess both complicated geometry and topology (i.e., many connected components and high genus). Because of their sheer size, efficient compression algorithms, in particular progressive encodings, are critical in working with these surfaces. Most standard mesh compression algorithms have been designed to deal with generally smooth surfaces of low topologic complexity. Much better results can be achieved with algorithms which are specifically designed for isosurfaces arising from volumetric datasets. We present a progressive encoding technique specifically designed for complex isosurfaces. It achieves better rate distortion performance than all standard mesh coders, and even improves on all previous single rate isosurface coders. Our novel algorithm handles isosurfaces with or without sharp features, and deals gracefully with high topologic and geometric complexity. The inside/outside function of the volume data is progressively transmitted through the use of an adaptive octree,while a local frame based encoding is used for the fine level placement of surface samples. Local patterns in topology and local smoothness in geometry are exploited by context-based arithmetic encoding,allowing us to achieve an average of 6.3 bits per vertex (b/v) at very low distortion. Of this rate only 0.69 b/v are dedicated to connectivity data: this improves by 18% over the best previous single rate isosurface encoder.

Discrete shells Discrete Shells (Eitan Grinspun, Anil Hirani, Mathieu Desbrun and Peter Schröder), Symposium on Computer Animation 2003. Abstract: In this paper we introduce a discrete shell model describing the behavior of thin flexible structures, such as hats, leaves, and aluminum cans, which are characterized by a curved undeformed configuration. Previously such models required complex continuum mechanics formulations and correspondingly complex algorithms. We show that a simple shell model can be derived geometrically for triangle meshes and implemented quickly by modifying a standard cloth simulator. Our technique convincingly simulates a variety of curved objects with materials ranging from paper to metal, as we demonstrate with several examples including a comparison of a real and simulated falling hat.

Subdivision surfaces can be tesselated on the GPU including support for features such as adaptive subdivision Evaluation of Subdivision Surfaces on Programmable Graphics Hardware (Jeff Bolz and Peter Schröder), submitted for publication. Abstract: High-order smooth surface primitives, such as subdivision patches for example, are attractive for the modeling of free-form surfaces. In contrast to meshes they require only a few control points to specify large sections of a surface. Unfortunately, much of this bandwidth advantage is lost when such surfaces have to be tessellated on the CPU prior to transmission over the graphics bus and rendering on the graphics card. For surfaces built through linear combination of basis functions it is possible to precompute tessellations and use these to evaluate the surface at runtime in a simple computation performed entirely on a programmable graphics processor (GPU). The improved bandwidth requirements - only control points need transmission during animation, for example - coupled with the high performance of GPUs, allows us to achieve tessellation rates up to 24 million vertices per second on a 500 MHz GeForce FX.

Multi-Chart Geometry Images Multi-Chart Geometry Images (P.V. Sander, Z.J. Wood, S. J. Gortler, J. Snyder, and H. Hoppe), Symposium on Geometry Processing 2003. Abstract: We introduce multi-chart geometry images, a new representation for arbitrary surfaces. It is created by resampling a surface onto a regular 2D grid. Whereas the original scheme of Gu et al. maps the entire surface onto a single square, we use an atlas construction to map the surface piecewise onto charts of arbitrary shape. We demonstrate that this added flexibility reduces parametrization distortion and thus provides greater geometric fidelity, particularly for shapes with long extremities, high genus, or disconnected components. Traditional atlas constructions suffer from discontinuous reconstruction across chart boundaries, which in our context create unacceptable surface cracks. Our solution is a novel zippering algorithm that creates a watertight surface. In addition, we present a new atlas chartification scheme based on clustering optimization.

3D data points and reconstructed spline surface From Scattered Samples to Smooth Surfaces (Kai Hormann), Proceedings of Geometric Modeling and Computer Graphics 2003. Abstract: The problem of reconstructing smooth surfaces from discrete scattered sample points arises in many fields of science and engineering and the data sources include measured values (laser range scanning, meteorology, geology) as well as experimental results (engineering, physics, chemistry) and computational values (evaluation of functions, finite element solutions, numerical simulations). We describe a processing pipeline that can be understood as gradually adding order to a given unstructured point cloud until it is completely organized in terms of a smooth surface. The individual steps of this pipeline are triangulation, remeshing, and surface fitting and have in common that they are much simpler to perform in two dimensions than in three. We therefore propose to use a parameterization in each of these steps so as to decrease the dimensionality of the problem and to reduce the computational complexity.

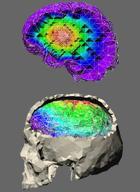
Ancient drinking cup and semi-regular reconstruction from a CT scan Hierarchical Iso-Surface Extraction (Ulf Labsik, Kai Hormann, Martin Meister, and Günther Greiner), JCISE, Vol. 2, Dec. 2002. Abstract: The extraction and display of iso-surfaces is a standard method for the visualization of volume data sets. In this paper we present a novel approach that utilizes a hierarchy on both the input and the output data.For the generation of a coarse base mesh, we construct a hierarchy of volumes and extract an iso-surface from the coarsest resolution with a standard Marching Cubes algorithm. We additionally apply a simple mesh decimation algorithm to improve the shape of the triangles. We iteratively fit this mesh to the iso-surface at the finer volume levels. To be able to reconstruct fine detail of the iso-surface we thereby adaptively subdivide the mesh. To evenly distribute the vertices of the triangle mesh over the iso-surface and generate a triangle mesh with evenly shaped triangles, we have integrated a mesh smoothing algorithm into the fitting process. The advantage of this approach is that it generates a mesh with subdivision connectivity which can be utilized by several multiresolution algorithms such as compression and progressive transmission. As applications of our method we show how to reconstruct the surface of archaeological artifacts and the reconstruction of the brain surface for the simulation of the brain shift phenomenon.


Examples of surfaces from a broad variety of application domains Subdivision as a Fundamental Building Block of Digital Geometry Processing Algorithms (Peter Schröder), appeared in Journal of Computational and Applied Mathematics Vol. 149, Dec. 2002. Abstract: Digital Geometry Processing (DGP) is a newly emerging discipline which aims to build the mathematical and algorithmic foundations for the next generation of digital multimedia. Digital signal processing was highly successful for earlier generations of digital multimedia such as sound, image, and video. Now that 3D scanning technologies make sampled surfaces broadly available a similar apparatus is needed to deal with this new multimedia datatype. Due to the inherent curvature of such surfaces though traditional tools are not immediately applicable. In this paper we give a brief overview of some recent developments in subdivision surfaces and how these help to build a foundation for DGP algorithms.

Fairing of wings and fin Data-Dependent Fairing of Subdivision Surfaces (Ilja Friedel, Patrick Mullen and Peter Schröder), appeared in Solid Modeling 2003. Abstract: In this paper we present a new algorithm for solving the data dependent fairing problem for subdivision surfaces, using Catmull-Clark surfaces as an example. Earlier approaches to subdivision surface fairing encountered problems with singularities in the parametrization of the surface. We address these issues through the use of the characteristic map parametrization, leading to well defined membrane and bending energies even at irregular vertices. Combining this approach with ideas from data-dependent energy operators we are able to express the associated nonlinear stiffness matrices for Catmull-Clark surfaces as linear combinations of precomputed energy matrices. This machinery also provides exact, inexpensive gradients and Hessians of the new energy operators. With these the nonlinear minimization problem can be solved in a stable and efficient way using Steihaug's Newton/CG trust-region method. We compare properties of linear and nonlinear methods through a number of examples and report on the performance of the algorithm. Download source codes (15MB, Linux).

Approximation error plot Data Dependent Energy Operators for Subdivision Surfaces (Ilja Friedel), Caltech M.S. thesis. Abstract: This thesis derives energies used in the "Data-Dependent Fairing of Subdivision Surfaces" paper. Approximation properties of the energies are examined in greater depth than it was possible in the paper.

Digital (0,2)-sequence Fast Generation of Randomized Low Discrepancy Point Sets (Ilja Friedel and Alexander Keller), Monte Carlo and Quasi-Monte Carlo Methods 2000, Springer-Verlag. Abstract: We introduce two novel techniques for speeding up the generation of digital (t,s)-sequences. Based on these results a new algorithm for the construction of Owen's randomly permuted (t,s)-sequences is developed and analyzed. An implementation of the new techniques is available.

Stretching a molecule with kitchen tongs Constructing a hairpin molecule in 3D Tangible + Virtual = A Flexible 3D Interface for Spatial Construction Applied to DNA (Steven Schkolne, Hiroshi Ishii, Peter Schröder), tech report. Abstract: Ideas from tangible interfaces and VR ease a difficult spatial design task: construct a DNA molecule with desired characteristics. Our hybrid interface has both the physical intimacy of tangible media and the versatility of 3D digital display. Two new physical affordances: a raygun and a grip tool, enable kinesthetic control of the addition and removal of structure. We introduce 3D local menus which select multiple functions for each tool. New interactions for sensed tongs enable the sophisticated multi-object arrangement that the delicate, intricate DNA construction task demands. These flexible tools allow UI designers to create multiple interfaces upon the same physical substrate. In a user study, practicing research scientists expressed a strong preference for Silkworm, our 3D interface, when compared to mouse + monitor UI. We show that 3D tangible interfaces, heretofore only applied to freeform artistic creation, also facilitate intuition in the highly structured task that is our focus.

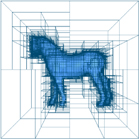
Pillows and balloons modeled with CHARMS. CHARMS: A Simple Framework for Adaptive Simulation (Eitan Grinspun, Petr Krysl and Peter Schröder), ACM TOG, 2002, (Proceedings of SIGGRAPH 2002). Abstract: Finite element solvers are a basic component of simulation applications; they are common in computer graphics, engineering, and medical simulations. Although adaptive solvers can be of great value in reducing the often high computational cost of simulations they are not employed broadly. Indeed, building adaptive solvers can be a daunting task especially for 3D finite elements. In this paper we are introducing a new approach to produce conforming, hierarchical, adaptive refinement methods (CHARMS). The basic principle of our approach is to refine basis functions, not elements. This removes a number of implementation headaches associated with other approaches and is a general technique independent of domain dimension (here 2D and 3D), element type (eg, triangle, quad, tetrahedron, hexahedron), and basis function order (piecewise linear, higher order B-splines, Loop subdivision, etc.). The (un-)refinement algorithms are simple and require little in terms of data structure support. We demonstrate the versatility of our new approach through 2D and 3D examples, including medical applications and thin-shell animations.

Adapted FEM model of brain tissue. Natural Hierarchical Refinement for Finite Element Methods (Petr Krysl, Eitan Grinspun, and Peter Schröder), International Journal for Numerical Methods in Engineering, 2003. Abstract: Current formulations of adaptive finite element mesh refinement seem simple enough, but their implementations prove to be a formidable task. We offer an alternative approach called CHARMS: Conforming Hierarchical Adaptive Refinement Methods. Our method yields equivalent adapted approximation spaces wherever the traditional mesh refinement is applicable, but proves to be significantly simpler to implement. At the same time it is much more powerful in that it is general (no special tricks are required for different types of finite elements), and applicable for some newer approximations where traditional mesh refinement concepts are not of much help, for instance on subdivision surfaces.

2K faced Buddha, before and after topology simplification Removing Excess Topology from Isosurfaces (Zoë Wood, Hugues Hoppe, Mathieu Desbrun, and Peter Schröder), ACM Transactions on Graphics, 23(2), April 2004. Abstract: Many high-resolution surfaces are created through isosurface extraction from volumetric representations, obtained by 3D photography, CT, or MRI. Noise inherent in the acquisition process can lead to geometrical and topological errors. Reducing geometrical errors during reconstruction is well studied. However, isosurfaces often contain many topological errors in the form of tiny topological handles. These nearly invisible artifacts hinder subsequent operations like mesh simplification, remeshing, and parameterization. In this paper we present an efficient method for removing topological handles in an isosurface. Our algorithm makes an axis-aligned sweep through the volume to locate handles, compute their sizes, and selectively remove them. The algorithm is designed for out-of-core execution. It finds the handles by incrementally constructing and analyzing a surface Reeb graph. The size of a handle is measured as the shortest surface loop that breaks it. Handles are removed robustly by modifying the volume rather than attempting "mesh surgery." Finally, the volumetric modifications are spatially localized to preserve geometrical detail. We demonstrate topology simplification on several complex models, and show its benefit for subsequent surface processing.

Dual sqrt3 subdivision applied to an irregular hex control mesh Composite Primal/Dual Sqrt(3)-Subdivision Schemes(Peter Oswald and Peter Schröder), Computer Aided Geometric Design, March 2003. Abstract: We present new families of primal and dual subdivision schemes for triangle meshes and Sqrt(3)-refinement. The proposed schemes use two simple local rules which cycle between primal and dual meshes a number of times. The resulting surfaces become very smooth at regular vertices if the number of cycles is > 1. The C1-property is violated only at low-valence irregular vertices, and can be restored by slight modifications of the local rules used.

As a generalization, we introduce a wide class of composite subdivision schemes suitable for arbitrary topologies and refinement rules. A composite scheme is defined by a simple upsampling from the coarse to a refined topology, embedded into a cascade of geometric averaging operators acting on coarse and/or refined topologies. We propose a small set of such averaging rules (and some of their parametric extensions) which allow for the switching between control nets associated with the same or different topologic elements (vertices, edges, faces), and show a number of examples, based on triangles, that the resulting class of composite subdivision schemes contains new and old, primal and dual schemes for Sqrt(3)-refinement as well as for quadrisection. As a common observation from the examples considered, we found that irregular vertex treatment is necessary only at vertices of low valence, and can easily be implemented by using generic modifications of some elementary averaging rules.


Examples of polygon meshes: (left) Beethoven mesh (2812 polygons, 2655 vertices) - (right) Galleon mesh (2384 polygons,2372 vertices). Near-Optimal Connectivity Encoding of 2-Manifold Polygon Meshes (Andrei Khodakovsky, Pierre Alliez, Mathieu Desbrun, Peter Schröder), to appear in a special issue of GMOD. Abstract: Encoders for triangle mesh connectivity based on enumeration of vertex valences are among the best reported to date. They are both simple to implement and report the best compressed file sizes for a large corpus of test models. Additionally they have recently been shown to be near-optimal since they realize the Tutte entropy bound for all planar triangulations. In this paper we introduce a connectivity encoding method which extends these ideas to 2-manifold meshes consisting of faces with arbitrary degree. The encoding algorithm exploits duality by applying valence enumeration to both the primal and dual mesh in a symmetric fashion. It generates two sequences of symbols, vertex valences and face degrees, and encodes them separately using two context-based arithmetic coders. This allows us to exploit vertex and/or face regularity if present. When the mesh exhibits perfect face regularity (e.g., a pure triangle or quad mesh) and/or perfect vertex regularity (valence six or four respectively) the corresponding bit rate vanishes to zero asymptotically. For triangle meshes, our technique is equivalent to earlier valence driven approaches. We report compression results for a corpus of standard meshes. In all cases we are able to show coding gains over earlier coders, sometimes as large as 50%. Remarkably, we even slightly gain over coders specialized to triangle or quad meshes. A theoretical analysis reveals that our approach is near-optimal as we achieve the Tutte entropy bound for arbitrary planar graphs of 2 bits per edge in the worst case.

Multivariate Approximation and Applications Subdivision, Multiresolution and the Construction of Scalable Algorithms in Computer Graphics (Peter Schröder), Multivariate Approximation and Applications, Cambridge University Press 2001. Abstract: Multiresolution representations are a critical tool in addressing complexity issues (time and memory) for the large scenes typically found in computer graphics applications. Many of these techniques are based on classical subdivision techniques and their generalizations. In this paper we review two exemplary applications from this area, multiresolution surface editing and semi-regular remeshing. The former is directed towards building algorithms which are fast enough for interactive manipulation of complex surfaces of arbitrary topology. The latter is concerned with constructing smooth parameterizations for arbitrary topology surfaces as they typically arise from 3D scanning techniques. Remeshing such surfaces then allows the use of classical subdivision ideas. We focus in particular on the practical aspects of making the well understood mathematical machinery applicable and accessible to the very general settings encountered in practice.

A tagged mesh subdivded to four levels and rendered with smooth shading. Rapid Evaluation of Catmull-Clark Subdivision Surfaces (Jeffrey Bolz, Peter Schröder), Web3D 2002 Symposium. Abstract: Using subdivision as a basic primitive for the construction of arbitrary topology, smooth, free-form surfaces is attractive for content destined for display on devices with greatly varying rendering performance. Subdivision naturally supports level of detail rendering and powerful compression algorithms. While the underlying algorithms are conceptually simple it is difficult to implement player engines which achieve optimal performance on modern CPUs such as the Intel Pentium family. In this paper we describe a novel table driven evaluation strategy for subdivision surfaces using as an example the scheme of Catmull and Clark. Cache conscious design and exploitation of SIMD instructions allows us to achieve nearly 100% FPU utilization in the inner loop and achieve a composite performance of 1.2 flop/cycle on the Intel PIII and 1.8 flop/cycle on the Intel P4 including all memory transfers. The algorithm supports tradeoffs between cache size and memory bus usage which we examine. A library which implements this engine is freely available from the authors.


A generic head model is fit to a Cyberware scan with 300k triangles. The resulting subdivision surface is edited to create a new facial expression. Fitting Subdivision Surfaces (Nathan Litke, Adi Levin, and Peter Schröder), Proceedings of Scientific Visualization 2001. Abstract: We introduce a new algorithm for fitting a Catmull-Clark subdivision surface to a given shape within a prescribed tolerance, based on the method of quasi-interpolation. The fitting algorithm is fast, local and scales well since it does not require the solution of linear systems. Its convergence rate is optimal for regular meshes and our experiments show that it behaves very well for irregular meshes. We demonstrate the power and versatility of our method with examples from interactive modeling, surface fitting, and scientific visualization.

An organic three-dimensional shape, drawn with the body in an immersive synthetic space. Drawing with the Hand in Free Space (Steven Schkolne), to be published in Leonardo August 2002 (submitted for review June 2000). Abstract: This article presents an artistic perspective on a medium for shape creation developed in collaboration with Michael Pruett and Peter Schröder (see below) Organic surfaces are drawn in 3d space with the hand. Additional tools move and deform the shape. Special interface hardware includes a head-tracked stereoscopic display and sensors which track the body and handheld tools, allowing the artist to share the space of the artwork. This method provides a fluid, unstructured access to 3d, ideal for quick, spontaneous ideation and investigation of complex structure.

Control mesh of a bent can, and self-interference regions on the limit surface resolved with increasing precision. Normal Bounds for Subdivision-Surface Interference Detection (Eitan Grinspun and Peter Schröder), Proceedings of IEEE Scientific Visualization, 2001. Abstract: Interference detection is vital for simulation and animation. Our interest was born of a larger project: using the Subdivision Element Method and the thin-shell equations we produce realistic animations of crushing, crumpling, and wrinkling. In this paper we derive normal bounds for subdivision surfaces and use these to develop an efficient algorithm for collision detection with specific optimizations for self-interference. The normal bounds are also useful for CAD and rendering.

Eight head scans have been parameterized onto the same base domain and resampled with the same sampling pattern, greatly facilitating operations such finding the average mesh. Consistent Mesh Parameterizations (Emil Praun, Wim Sweldens, and Peter Schröder), Siggraph 2001. Abstract: A basic element of Digital Geometry Processing algorithms is the establishment of a smooth parameterization for a given model. In this paper we propose an algorithm which establishes parameterizations for a set of models. The parameterizations are called consistent because they share the same base domain and respect features. They give immediate correspondences between models and allow remeshes with the same connectivity. Such remeshes form the basis for a large class of algorithms, including principal component analysis, wavelet transforms, detail and texture transfer between models, and n-way shape blending. We demonstrate the versatility of our algorithm with a number of examples.

Topological changes in a hybrid mesh of Buddha. Hybrid Meshes: Multiresolution using regular and irregular refinement (Igor Guskov, Andrei Khodakovsky, Peter Schröder, and Wim Sweldens), Proceedings of SoCG 2002. Abstract: A hybrid mesh is a multiresolution surface representation that combines advantages from regular and irregular meshes. Irregular operations allow a hybrid mesh to change topology throughout the hierarchy and approximate detailed features at multiple scales. A preponderance of regular refinements allows for efficient data-structures and processing algorithms. We provide a user driven procedure for creating a hybrid mesh from scanned geometry and present a progressive hybrid mesh compression algorithm.

Hand motion is used to create surfaces on the Responsive Workbench. Surface Drawing: Creating Organic 3D Shapes with the Hand and Tangible Tools (Steven Schkolne, Michael Pruett, Peter Schröder), CHI 2001. Abstract: Surface Drawing is a system for creating organic 3D shapes in a manner which supports the needs and interests of artists. This medium facilitates the early stages of creative design which many 3D modeling programs neglect. Much like traditional media such as line drawing and painting, Surface Drawing lets users construct shapes through repeated marking. In our case, the hand is used to mark 3D space in a semi-immersive virtual environment. The interface is completed with tangible tools to edit and manipulate models. We introduce the use of tongs to move and scale 3D shapes and demonstrate a magnet tool which is comfortably held without restricting hand motion. We evaluated our system through collaboration with artists and designers, exhibition before hundreds of users, our own extensive exploration of the medium, and an informal user study. Response was especially positive from users with an artistic background.

Buddha: genus 104, dragon: genus 46, David's head: genus 340. (all models courtesy Stanford University) Topological Noise Removal (Igor Guskov and Zoë Wood), Proceedings of Graphics Interface 2001. Abstract: Meshes obtained from laser scanner data often contain topological noise due to inaccuracies in the scanning and merging process. This topological noise complicates subsequent operations such as remeshing, parameterization and smoothing. We introduce an approach that removes unnecessary nontrivial topology from meshes. Using a local wave front traversal, we discover the local topologies of the mesh and identify features such as small tunnels. We then identify non-separating cuts along which we cut and seal the mesh, reducing the genus and thus the topological complexity of the mesh.

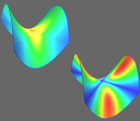Mean (top left) and max (bottom right) curvature plots of a triangulated saddle using pseudocolors Discrete Differential-Geometry Operators for Triangulated 2-Manifolds (Mark Meyer, Mathieu Desbrun, Peter Schröder and Alan H. Barr), VisMath 2002. Abstract: This paper provides a consistent set of flexible tools to approximate important geometric attributes, including normal vectors and curvatures, on arbitrary 2D and 3D meshes embedded in n dimensions. We present a consistent derivation of these first and second order differential properties using Voronoi cells and the mixed Finite Element/Finite Volume method. The new operators are closely related to the continuous case, guaranteeing an appropriate extension from the continuous to the discrete setting: they respect the intrinsic properties of the continuous differential opeators. We show that these estimates are optimal in accuracy under mild smoothness conditions, and demonstrate their numerical quality. We finally present applications of these operators, such as mesh smoothing and enhancement, quality checking, and denoising of arbitrary vector fields, such as flow fields or tensor images.

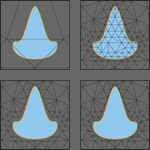Four steps in our trimming procedure. Trimming for Subdivision Surfaces (Nathan Litke, Adi Levin and Peter Schröder), CAGD 2002. Abstract: Trimming is an important primitive operation in geometric modeling. It is also the root of many numerical and topological problems in modern NURBS based CAGD systems. In this paper we introduce a new method for trimming subdivision surfaces. It is based on the use of combined subdivision schemes to guarantee exact interpolation of trim curves. The latter ensures, for example, that if two surfaces share a trim curve, they will meet exactly at the trim curve. In contrast to traditional approaches to trimming (e.g., for NURBS) we construct a new control mesh with each trim operation. This causes a perturbation of the surface near the trim region, which we control through the use of multiresolution details. These are computed rapidly and at low cost with the help of a novel set of quasi-interpolation operators. We demonstrate our algorithm with a number of examples.

Repeated averaging subdivision of orders 3, 5, 7 and 9 applied to a pipe shape (top left to bottom right). A Unified Framework for Primal/Dual Quadrilateral Subdivision Schemes (Denis Zorin and Peter Schröder), CAGD 2002. Abstract: Quadrilateral subdivision schemes come in primal and dual varieties, splitting faces or respectively vertices. The scheme of Catmull-Clark is an example of the former, while the Doo-Sabin scheme exemplifies the latter. In this paper we consider the construction of an increasing sequence of alternating primal/dual quadrilateral subdivision schemes based on a simple averaging approach. Beginning with a vertex split step we successively construct variants of Doo-Sabin and Catmull-Clark schemes followed by novel schemes generalizing B-splines of bidegree up to nine. We prove the schemes to be C1 at irregular surface points, and analyze the behavior of the schemes as the number of averaging steps increases. We discuss a number of implementation issues common to all quadrilateral schemes. In particular we show how both primal and dual quadrilateral schemes can be implemented in the same code, opening up new possibilities for more flexible geometric modeling applications and p-versions of the Subdivision Element Method. Additionally we describe a simple algorithm for adaptive subdivision of dual schemes.

Tail section of semi-regular mesh of feline, showing nontrivial topology
Marching cubes extraction of the same mesh
Semi-Regular Mesh Extraction from Volumes (Zoë Wood, Mathieu Desbrun, Peter Schröder and David Breen), Proceedings of Visualization 2000. Abstract: We present a novel method to extract iso-surfaces from distance volumes. It generates high quality semi-regular multiresolution meshes of arbitrary topology. Our technique proceeds in two stages. First, a very coarse mesh with guaranteed topology is extracted. Subsequently an iterative multi-scale force-based solver refines the initial mesh into a semi-regular mesh with geometrically adaptive sampling rate and good aspect ratio triangles. The coarse mesh extraction is performed using a new approach we call surface wavefront propagation. A set of discrete iso-distance ribbons are rapidly built and connected while respecting the topology of the iso-surface implied by the data. Subsequent multi-scale refinement is driven by a simple force-based solver designed to combine good iso-surface fit and high quality sampling through reparameterization. In contrast to the Marching Cubes technique our output meshes adapt gracefully to the iso-surface geometry, have a natural multiresolution structure and good aspect ratio triangles, as demonstrated with a number of examples.

Bug hoods optimized with respect to weight and stiffness using this shell modeling with subdivision surfaces Integrated Modeling, Finite-Element Analysis, and Design for Thin-Shell Structures using Subdivision (Fehmi Cirak, Michael Scott, Peter Schröder, Michael Ortiz and Erik Antonsson), CAD 2002. Abstract: Many engineering design applications require geometric modeling and mechanical simulation of thin flexible structures, such as those found in the automotive and aerospace industries. Traditionally, geometric modeling, mechanical simulation, and design are treated as separate modules requiring different methods and representations. Combining them into a common design environment leads to many difficulties due to the incompatibility of the involved representations. We propose the use of subdivision surfaces as a common foundation for modeling, simulation, and design in a unified framework. Subdivision surfaces provide a flexible and efficient tool for arbitrary topology free form surface modeling, avoiding many of the problems inherent in traditional spline patch based approaches. The underlying basis functions are also ideally suited for a finite element treatment of the so-called thin shell equations, which describe the mechanical behavior of the modeled structures. The resulting solvers are highly scalable, providing an efficient computational foundation for design exploration and optimization. We demonstrate our claims with several design examples, showing the versatility and high accuracy of the proposed method.

Partial reconstructions from a progressive encoding of the dinosaur. File sizes are 549B(left) 1225B (middle) 18111B (right) Normal Mesh Compression (Andrei Khodakovsky and Igor Guskov), Geometric Modeling for Scientific Visualization, Springer-Verlag, Heidelberg, Germany, 2002.Abstract: Normal meshes were recently introduced as a new way to represent geometry. A normal mesh is a multiresolution representation which has the property that all details lie in a known normal direction and hence the mesh depends only on a single scalar per vertex. Such meshes are ideally suited for progressive compression. We demonstrate such a compression algorithm for normal meshes representing complex, arbitrary topology surfaces as they appear in 3D scanning and scientific visualization. The resulting coder is shown to exhibit gains of an additional 2-5dB over the previous state of the art.

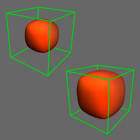Different Subdivision schemes Subdivision for Modeling and Animation course notes for SIGGRAPH 2000 (Denis Zorin and Peter Schröder, Eds., with Adi Levin, Leif Kobbelt, Wim Sweldens, and Tony DeRose). This course is an advanced introduction to subdivision and its applications in computer graphics. It gives all the mathematical details needed by implementors, but skips most of the proofs.

Raw (noisy) Mars elevation map After non-uniform anisotropic noise diffusion Anisotropic Feature-Preserving Denoising of Height Fields and Bivariate Data (Mathieu Desbrun, Mark Meyer, Peter Schröder and Alan H. Barr), Graphics Interface 2000. Abstract: In this paper, we present an efficient way to denoise bivariate data like height fields, color pictures or vector fields, while preserving edges and other features. Mixing surface area minimization, graph flow, and nonlinear edge-preservation metrics, our method generalizes previous anisotropic diffusion approaches in image processing, and is applicable to data of arbitrary dimension. Another notable difference is the use of a more robust discrete differential operator, which captures the fundamental surface properties. We demonstrate the method on range images and height fields, as well as greyscale or color images.

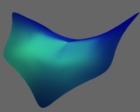Loop subdivision surface near a vertex of valence eight with eigenvalues such that the principal curvatures are no smoother than square integrable. Curvature Integrability of Subdivision Surfaces (Ulrich Reif and Peter Schröder), Advances in Computational Mathematics, 14(2), 2001. Abstract: We examine the smoothness properties of the principal curvatures of subdivision surfaces near extraordinary points. In particular we give an estimate of their Lp class based on the eigen structure of the subdivision matrix. As a result we can show that the popular Loop and Catmull-Clark schemes (among many others) have square integrable principal curvatures justifying their use as shape functions in FEM treatments of the thin shell equations.

Partial reconstructions of the progressive bitstream of the Venus head model at 476B (bytes), 1528B, 4163B, and 26800B. Progressive Geometry Compression (Andrei Khodakovsky, Peter Schröder and Wim Sweldens), Proceedings of SIGGRAPH 2000 Abstract: We propose a new progressive compression scheme for arbitrary topology, highly detailed and densely sampled meshes arising from geometry scanning. We observe that meshes consist of three distinct components: geometry, parameter, and connectivity information. The latter two do not contribute to the reduction of error in a compression setting. Using semi-regular meshes, parameter and connectivity information can be virtually eliminated. Coupled with semi-regular wavelet transforms, zerotree coding, and subdivision based reconstruction we see improvements in error by a factor four (12dB) compared to other progressive coding schemes.

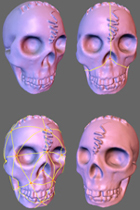On the top left the original skull dataset with 3 floats per vertex. Going through two intermediate stages we construct a normal mesh (bottom right) with only 1 float per vertex. Normal Meshes (Igor Guskov, Kiril Vidimce, Wim Sweldens and Peter Schröder), Proceedings of SIGGRAPH 2000 Abstract: Normal meshes are new fundamental surface descriptions inspired by differential geometry. A normal mesh is a multiresolution mesh where each level can be written as a normal offset from a coarser version. Hence the mesh can be stored with a single float per vertex. We present an algorithm to approximate any surface arbitrarily closely with a normal semi-regular mesh. Normal meshes are useful in numerous applications such as compression, filtering, rendering, texturing, and modeling.

Cylinder Example Subdivision Surfaces: A New Paradigm for Thin-Shell Finite-Element Analysis (Fehmi Cirak and Michael Ortiz and Peter Schröder), International Journal for Numerical Methods in Engineering. Abstract: We develop a new paradigm for thin-shell finite-element analysis based on the use of subdivision surfaces for: i) describing the geometry of the shell in its undeformed configuration, and ii) generating smooth interpolated displacement fields possessing bounded energy within the strict framework of the Kirchhoff-Love theory of thin shells. The particular subdivision strategy adopted here is Loop's scheme, with extensions such as required to account for creases and displacement boundary conditions. The displacement fields obtained by subdivision are H2 and, consequently, have a finite Kirchhoff-Love energy. The resulting finite elements contain three nodes and element integrals are computed by a one-point quadrature. The displacement field of the shell is interpolated from nodal displacements only. In particular, no nodal rotations are used in the interpolation. The interpolation scheme induced by subdivision is nonlocal, i.e., the displacement field over one element depend on the nodal displacements of the element nodes and all nodes of immediately neighboring elements. However, the use of subdivision surfaces ensures that all the local displacement fields thus constructed combine conformingly to define one single limit surface. Numerical tests, including the Belytschko et al. obstacle course of benchmark problems, demonstrate the high accuracy and optimal convergence of the method.

Denoising the output of a 3D scanning system is one of the primary applications of our techniques. Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow (Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan Barr), Proceedings of SIGGRAPH 99. Abstract: In this paper, we develop methods to rapidly remove rough features from irregularly triangulated data intended to portray a smooth surface. The main task is to remove undesirable noise and uneven edges while retaining desirable geometric features. The problem arises mainly when creating high-fidelity computer graphics objects using imperfectly-measured data from the real world.

Our approach contains three novel features: an implicit integration method to achieve efficiency, stability, and large time-steps; a scale-dependent Laplacian operator to improve the diffusion process; and finally, a robust curvature flow operator that achieves a smoothing of the shape itself, distinct from any parameterization. Additional features of the algorithm include automatic exact volume preservation, and hard and soft constraints on the positions of the points in the mesh.

We compare our method to previous operators and related algorithms, and prove that our curvature and Laplacian operators have several mathematically-desirable qualities that improve the appearance of the resulting surface. In consequence, the user can easily select the appropriate operator according to the desired type of fairing. Finally, we provide a series of examples to graphically and numerically demonstrate the quality of our results.


Morph from the mannequin head to the venus. Multiresolution Mesh Morphing (Aaron Lee, David Dobkin, Wim Sweldens, and Peter Schröder), Proceedings of SIGGRAPH 99. Abstract: We present a new method for user controlled morphing of two homeomorphic triangle meshes of arbitrary topology. In particular we focus on the problem of establishing a correspondence map between source and target meshes. Our method employs the MAPS algorithm to parameterize both meshes over simple base domains and an additional harmonic map bringing the latter into correspondence. To control the mapping the user specifies any number of feature pairs, which control the parameterizations produced by the MAPS algorithm. Additional controls are provided through a direct manipulation interface allowing the user to tune the mapping between the base domains. We give several examples of esthetically pleasing morphs which can be created in this manner with little user input. Additionally we demonstrate examples of temporal and spatial control over the morph.

Curvature plot around an extraordinary vertex with valence 8 with the original Loop scheme (top) and a bounded curvature modification (bottom). Subdivision for Modeling and Animation course notes for SIGGRAPH 99 (Denis Zorin and Peter Schröder, Eds., with Jos Stam, Leif Kobbelt, Joe Warren, and Tony DeRose). This course is an advanced introduction to subdivision and its applications in computer graphics. It gives all the mathematical details needed by implementors, but skips most of the proofs. Next to Joe Warren's monograph this is a good place to get started if you want to learn about subdivision.

Smooth function constructed over an irregular mesh. Wavelets on Irregular Point Sets (Ingrid Daubechies, Igor Guskov, Peter Schröder, and Wim Sweldens), Phil. Trans. R. Soc. Lond. A., pp 2397--2413, number 357. Abstract: In this article we review techniques for building and analyzing wavelets on irregular point sets in one and two dimensions. We discuss current results both on the practical and theoretical side. In particular we focus on subdivision schemes and commutation rules. Several examples are included.

Virtual surgery: using adaptive resolution to achieve realtime animation Interactive Multiresolution Animation of Deformable Models (Gilles Debunne, Mathieu Desbrun, Al Barr, Marie-Paule Cani), Proceedings of Eurographics Workshop on Computer Animation and Simulation'99. Abstract: This paper presents an approach to animate elastic deformable ma-terials at interactive rates using space-time adaptive resolution. We propose a new computational model, based on the conventional Hooke's law, that uses a discrete approximation of derivative opera-tors on irregular sample points. It allows local refinement or simplification of the computational model based on local error measure-ment. We in effect minimize calculations while ensuring a realistic and scale-independent behavior within a given accuracy threshold. We demonstrate this technique on a real-time virtual liver surgery application.

A silk scarf moved around a virtual scene, captured during a live session on the workbench. Interactive Animation of Structured Deformable Objects (Mathieu Desbrun, Peter Schröder, Al Barr), Proceedings of Graphics Interface '99. Abstract: In this paper, we propose a stable and efficient algorithm for animating mass-spring systems. An integration scheme derived from implicit integration allows us to obtain interactive realistic animation of any mass-spring network. We alleviate the need to solve a linear system through the use of a predictor-corrector approach: We first compute a rapid approximation of the implicit integration, then we correct this estimate in a post-step process to preserve momentum. Combined with an inverse dynamics process to implement collisions and other constraints, this method provides a simple, stable and tunable model for deformable objects suitable for virtual reality. An implementation in a VR environment demonstrates this approach.

The natural expression of this bird was easily developed with the new medium of Surface Drawing Surface Drawing (Steven Schkolne and Peter Schröder), Caltech Computer Science CS-TR-99-03 Abstract: Surface Drawing is a new medium which provides direct control over the creation of a wide range of intricate shapes. Surface Drawing addresses several key issues in creative expression and perceptual thinking by providing a direct link between the motions of the hand and the forging of shapes. Surfaces are created by moving a hand, instrumented with a special glove, through space in a semi-immersive 3D display and interaction environment (the Responsive Workbench). This technique allows both novices and experts to create intricate forms without the perceptual constraints of a rigid mathematical structure, large toolset, or a reduction of modeling to editing. In Surface Drawing the design space can be freely explored during the modeling process without the need to plan the construction of the final shape. In particular it supports unconstrained erasing and buildup of new geometry. This is achieved through the use of a novel incremental construction method for triangulated meshes, the Cookie Cutter algorithm. It allows the user to freely grow, join, and erase surfaces based on hand motions. We report on our experiences with the system and present results created by artists and designers exploring problems in industrial design, character design, and fine art.

Design study for a bicycle helmet using multiresolution geometry enhanced with feature editing Fine Level Feature Editing for Subdivision Surfaces (Andrei Khodakovsky and Peter Schröder), Proceedings of ACM Solid Modeling '99. Abstract: In many industrial design modeling scenarios the designer wishes to edit small feature lines - such as variable width and height creases - on otherwise smooth surface patches. When the path of such a feature does not align with an iso-parameter line or crosses patch boundaries it becomes increasingly difficult to maintain good editing semantics of the underlying surface. In this paper we describe an algorithm and implementation allowing the interactive creation and manipulation of fine scale feature curves on subdivision surfaces. In particular, our approach addresses the problem of defining the path of such feature curves independent of the location of surface iso-parameter lines and global patch boundaries. The feature lines are modeled as swept displacement curves with variable profiles, providing a rich toolbox of shapes. Furthermore, the hierarchical editing semantics of subdivision surface based representations carry through to our extended setting, ensuring "good" behavior of the feature lines under coarse scale surface edits.

Multiresolution edited and frequency enhanced cow given as an arbitrary connectivity mesh. Multiresolution Signal Processing for Meshes (Igor Guskov, Wim Sweldens, Peter Schröder), Proceedings of SIGGRAPH 99. Abstract: We generalize basic signal processing tools such as downsampling, upsampling, and filters to irregular connectivity 3D triangular meshes. This is accomplished through the design of a non-uniform relaxation procedure whose weights depend on the geometry and we show its superiority over existing schemes whose weights only depend on connectivity. This is combined with known mesh simplification methods to build subdivision, pyramid, and wavelet algorithms. We demonstrate the power of these algorithms through a number of application examples including smoothing, enhancement, editing, and texture mapping.

Adaptive, multiresolution representation of a machine part with exactly resolved features (edges, corners) and guaranteed error (1%) MAPS: Multiresolution Adaptive Parameterization of Surfaces (Aaron Lee, Wim Sweldens, Peter Schröder, Lawrence Cowsar, David Dobkin), Proceedings of SIGGRAPH 98. Abstract: We construct smooth parameterizations of irregular connectivity triangulations of arbitrary genus 2-manifolds. Our algorithm uses hierarchical simplification to efficiently induce a parameterization of the original mesh over a base domain consisting of a small number of triangles. This initial parameterization is further improved through a hierarchical smoothing procedure based on Loop subdivision applied in the parameter domain. Our method supports both fully automatic and user constrained operations. In the latter, we accommodate point and edge constraints to force the alignment of iso-parameter lines with desired features. We show how to use the parameterization for fast, hierarchical subdivision connectivity remeshing with guaranteed error bounds. The remeshing algorithm constructs an adaptively subdivided mesh directly without first resorting to uniform subdivision followed by subsequent sparsification. It thus avoids the exponential cost of the latter. Our parameterizations are also useful for texture mapping and morphing applications, among others.

An active implicit surface coating a particle system. Active Implicit Surface for Animation (Mathieu Desbrun, Marie-Paule Cani), Proceedings of Graphics Interface '98. Abstract: This paper introduces a new model of deformable surfaces designed for animation, which we call active implicit surfaces. The underlying idea is to animate a potential field defined by discrete values stored in a grid, rather than directly animating a surface. This surface, defined as an iso-potential of the field, has the ability to follow a given object using a snake-like strategy. Surface tension and other characteristics such as constant surface area or constant volume may be added to this model. The implicit formulation allows the surface to easily experience topology changes during simulation. We present an optimized implementation: computations are restricted to a close neighborhood around the surface. Applications range from the coating of deformable materials simulated by particle systems (the surface hides the granularity of the underlying model) to the generation of metamorphosis between shapes that may not have the same topology.

Comparison of curvature distribution along two alternative interpolatory subdivision schemes A Multiresolution Framework for Vatiational Subdivision (Leif Kobbelt and Peter Schröder), TOG, 17(4), pp 209--237 (previously available as CS-TR-97-05 under the title: Constructing Variationally Optimal Curves using Subdivision). Abstract: Subdivision is a powerful paradigm for the generation of curves and surfaces. It is easy to implement, computationally efficient, and useful in a variety of applications because of its intimate connection with multiresolution analysis. An important task in computer graphics and geometric modeling is the construction of curves that interpolate a given set of points and minimize a fairness functional (variational design). In the context of subdivision, fairing leads to special schemes requiring the solution of a banded linear system at every subdivision step. We present several examples of such schemes including one that reproduces non-uniform interpolating cubic splines. Expressing the construction in terms of certain elementary operations we are able to embed variational subdivision in the lifting framework, a powerful technique to construct wavelet filter banks given a subdivision scheme. This allows us to extend the traditional lifting scheme for FIR filters to a certain class of IIR filters. Consequently we show how to build variationally optimal curves \emph{and} associated, stable wavelets in a straightforward fashion. The algorithms to perform the corresponding decomposition and reconstruction transformations are easy to implement and efficient enough for interactive applications.

Multiresolution Editor Interactive Multiresolution Mesh Editing (Denis Zorin, Peter Schröder and Wim Sweldens), Proceedings of SIGGRAPH 1997. Abstract: We describe a multiresolution representation for meshes based on subdivision, which is a natural extension of the existing patch-based surface representations. Combining subdivision and the smoothing algorithms of Taubin (1995) allows us to construct a set of algorithms for interactive multiresolution editing of complex hierarchical meshes of arbitrary topology. The simplicity of the underlying algorithms for refinement and coarsification enables us to make them local and adaptive, thereby considerably improving their efficiency. We have built a scalable interactive multiresolution editing system based on such algorithms.

Retouched version of Prof. Schröder's license plate from South Carolina (no kidding!) Wavelets in Computer Graphics course notes for Siggraph 96 (Peter Schröder, Wim Sweldens, Michael Cohen, Tony DeRose, and David Salesin). The first two chapters are the latest (and much improved...) guide to "Building Your Own Wavelets at Home." (Wim Sweldens and Peter Schröder)

Control polyhedron on left; limit surface on right Interpolating Subdivision for Meshes with Arbitrary Topology (Denis Zorin, Peter Schröder, and Wim Sweldens), appeared in Proceedings of Siggraph 1996 (Extended TR version). Abstract: Subdivision is a powerful paradigm for the generation of surfaces of arbitrary topology. Given an initial triangular mesh the goal is to produce a smooth and visually pleasing surface whose shape is controlled by the initial mesh. Of particular interest are interpolating schemes since they match the original data exactly, and are crucial for fast multiresolution and wavelet techniques. Dyn, Gregory, and Levin introduced the Butterfly scheme [90], which yields C^1 surfaces in the topologically regular setting. Unfortunately it exhibits undesirable artifacts in the case of an irregular topology. We examine these failures and derive an improved scheme, which retains the simplicity of the Butterfly scheme, is interpolating, and results in smoother surfaces.

Transition of diffuse to highly specular reflection simulated with a wavelet solver Wavelets in Computer Graphics (Peter Schröder) appeared in Proceedings of the IEEE, Vol 84, No. 4, 1996 pp 615--625. Abstract: One of the perennial goals in computer graphics is realism in realtime. Handling geometrically complex scenes and physically faithful descriptions of their appearance and behavior, clashes with the requirement of multiple frame per second update rates. It is no surprise then that hierarchical modeling and simulation have already enjoyed a long history in computer graphics. Most recently these ideas have received a significant boost as wavelet based algorithms have entered many areas in computer graphics. We give an overview of some of the areas in which wavelets have already had an impact on the state of the art.

Linear (left) and Butterfly (right) spherical scaling functions (top) and wavelets (bottom) Spherical Wavelets: Efficiently Representing Functions on the Sphere (Peter Schröder and Wim Sweldens), appeared in Proceedings of Siggraph 95. Abstract: Wavelets have proven to be powerful bases for use in numerical analysis and signal processing. Their power lies in the fact that they only require a small number of coefficients to represent general functions and large data sets accurately. This allows compression and efficient computations. Classical constructions have been limited to simple domains such as intervals and rectangles. In this paper we present a wavelet construction for scalar functions defined on the sphere. We show how biorthogonal wavelets with custom properties can be constructed with the lifting scheme. The bases are extremely easy to implement and allow fully adaptive subdivisions. We give examples of functions defined on the sphere, such as topographic data, bidirectional reflection distribution functions, and illumination, and show how they can be efficiently represented with spherical wavelets.

Reflection mapped sphere (left) with wavelet processed spherical texture (right) Spherical Wavelets: Texture Processing (Peter Schröder and Wim Sweldens), appeared in Rendering Techniques `95, Springer Verlag. Abstract: Wavelets are a powerful tool for planar image processing. The resulting algorithms are straightforward, fast, and efficient. With the recently developed spherical wavelets this framework can be transposed to spherical textures. We describe a class of processing operators which are diagonal in the wavelet basis and which can be used for smoothing and enhancement. Since the wavelets (filters) are local in space and frequency, complex localized constraints and spatially varying characteristics can be incorporated easily. Examples from environment mapping and the manipulation of topography/bathymetry data are given.

Wavelet radiosity solution of environment with reflective and emissive textures Textures and Radiosity: Controlling Emission and Reflection with Texture Maps, (Reid Gershbein, Peter Schröder, and Pat Hanrahan), appeared in Proceedings of Siggraph 94. Abstract: In this paper we discuss the efficient and accurate incorporation of texture maps into a hierarchical Galerkin radiosity algorithm. This extension of the standard algorithm allows the use of textures to describe complex reflectance and emittance patterns over surfaces, increasing the realism and complexity of radiosity images. Previous approaches to the inclusion of textures have either averaged the texture to yield a single color for the radiosity computations, or exhaustively generated detail elements - possibly as many as one per texture pixel. The former does not capture important lighting effects due to textures, while the latter is too expensive computationally to be practical. We show how to incorporate textures into a wavelet radiosity solver at very little overhead and with guaranteed error bounds.

Wired Wavelet Image Compression (Peter Schröder) appeared in Wired Magazine, 3.05, May 1995.

Exact solution for form factor between two quads at arbitrary angle theta as function of aspect ratio On the Formfactor between Two Polygons (Peter Schröder and Pat Hanrahan), appeared in Proceedings of Siggraph 93 (extended TR version, Mathematica Code, C library). Abstract: Form factors are used in radiosity to describe the fraction of diffusely reflected light leaving one surface and arriving at another. They are a fundamental geometric property used for computation. Many special configurations admit closed form solutions. However, the important case of the form factor between two polygons in three space has had no known closed form solution. We give such a solution for the case of general (planar, convex or concave, possibly containing holes) polygons.
Copyright 1995-2011 Peter Schröder